|
|
|
|
|
|
|
|

| Disclaimer Information in this document is provided in connection with Intel products. No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted by this document. Except as provided in Intel's Terms and Conditions of Sale for such products, Intel assumes no liability whatsoever, and Intel disclaims any express or implied warranty, relating to sale and/or use of Intel products including liability or warranties relating to fitness for a particular purpose, merchantability, or infringement of any patent, copyright or other intellectual property right. Intel products are not intended for use in medical, life saving, or life sustaining applications. Intel may make changes to specifications and product descriptions at any time, without notice. Copyright © Intel Corporation (1996). Third-party brands and names are the property of their respective owners.
|
The purpose of three-dimensional (3D) computer graphics is to generate the best possible rendition of 3D objects on a two-dimensional (2D) computer screen (or other output device). Good rendition is achieved by accurately modeling the physical properties (geometry, shading, color, texture, etc.) of 3D scenes and objects. Better modeling accuracy generates better images, but requires more computation. Processing power is presently the limiting factor in 3D image quality, especially for 3D animation, which requires scenes to be computed and rendered in fixed, small amounts of time. Any increase in processing power can enable more complex scenes, better detailed objects, and/or smoother animation.
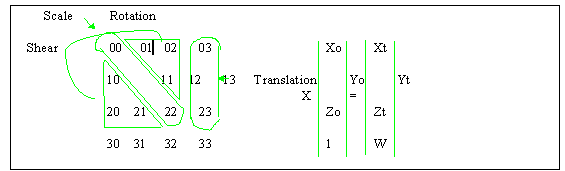
Common geometrical transforms include Translation (change of position), Rotation (change of angle), Scale (change of size) and Shear (linearly dependent change of position). It is convenient to write the transform of points in terms of matrix multiplication of vectors, as in Example 1.
_ _ _ _ _ _ | Transform | x | original | = | transformed | | Matrix | | vector | | vector | - - - - - -
For 3D space, each transform has a component in each
of the three dimensions (x,
y and z), and
can be written as a 4x4 matrix (see Example 2). Vector size is
chosen to be
4x1 ([x, y, z, 1]T), to match the 4x4 matrix
size.
Translation (T) Scale (S) Shear (H)(Th = translation along h axis) (Sh = scaling along h axis) (Hhm = dependence h on m)
1 0 0 Tx Sx 0 0 0 1 Hxy Hxz 0
0 1 0 Ty 0 Sy 0 0 Hyx 1 Hyz 0
0 0 1 Tz 0 0 Sz 0 Hzx Hzy 1 0
0 0 0 1 0 0 0 1 0 0 0 1
Rotation about x (Rx) Rotation about y (Ry) Rotation about z (Rz)
( Cx = cos(angle), (Cy = cos(angle), (Cz =cos(angle),
Ix = sin(angle) ) Iy = sin(angle)) Iz = sin(angle))
1 0 0 0 Cy 0 Iy 0 Cz Iz 0 0
0 Cx Ix 0 0 1 0 0 -Iz Cz 0 0
0 -Ix Cx 0 -Iy 0 Cy 0 0 0 1 0
0 0 0 1 0 0 0 1 0 0 0 1
All of these transforms can be combined into a single 4x4 matrix, by matrix multiplication:
Large objects are modeled by many polygons (usually triangles or rectangles) which are, in turn, defined by their vertices (3D points). An entire object (or group of objects) is transformed by applying a given transform to each of its vertices. Thus it is efficient to calculate M once (per animation frame and/or per object), then apply its results to many vertices:
where Voi is the i-th original vector, and Vti is the i-th transformed vector.
Since the number of vertices (i) is typically large, 3D geometry performance becomes largely dependent on the speed of this series of matrix-vector multiplies, making matrix-vector multiplication a worthwhile candidate for MOVD optimization.
The transformation matrix M, original vector(s) Voi, and transformed vector(s) Vti, (described above) have the form shown in Figure 1.
Each matrix-vector multiplication amounts to a series of vector-vector (dot product) multiplications, each of which is a series of scalar multiplies and adds:
MMX technology provides acceleration through Single Instruction Multiple Data (SIMD) parallelism, where either two 32-bit, four 16-bit or eight 8-bit integer values are operated on at once. SIMD multiplication and SIMD addition instructions are provided. Furthermore, one MMX instruction, PMADDWD, performs both multiply and add, on four 16-bit values simultaneously. This instruction is an excellent match to the four-element multiply/adds shown above. Its 16-bit integer precision is generally Section 3.1 for more details.)
Most of a vector-vector multiplication can be accomplished by a PMADDWD instruction. Since PMADDWD leaves the answer in two halves, a shift and an add instruction are used to complete the calculation. One vector-vector multiplication (for Xt) is diagrammed in Figure 2.
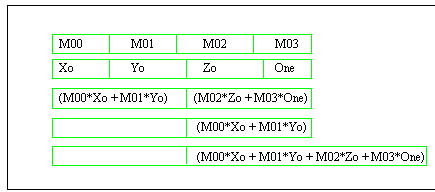
At this point, the answer is 32 bits long (occupying bits 0-29, with sign extended in bits 0-31). A shift of (nominally) 15 bits is required to return this answer to the original 16-bit size. The least significant 15 bits are lost, leaving data in bits 0-15, and sign in bit 16. More details of this shift are discussed in the next section.
The final (scalar) sum is the first element of the transformed (result) vector. This sequence must be repeated for each matrix row, to generate each element of the transformed vector.
Notice that the last row of M is essentially unused. (Occasionally this row is used in certain types of warping, but this is uncommon.) This row (and its calculations) can be omitted, for about 25% savings in calculations.
Since M is constant, its three rows can be loaded once, using 64-bit reads, and held in three 64-bit MM registers. (Assuming that no better use is found for the three MM registers.)
Each input vector (Voi) is read once, using a 64-bit read.
The results (16-bit integer elements of Vti) are written to memory individually. Memory writes from MMX registers are either 64- or 32-bit writes. 64-bit writes are no advantage in this algorithm because of the extra cycles that would be required to combine three or four 16-bit integers into a 64-bit word.
Pseudocode for the algorithm is given in Example 3.
MatrixVectMult (ptr to M, ptr to Vo, number of Vo, ptr to Vt) Get passed parameters (pointers) Read Rows of M into mm regs MxV: Read Voi into mm reg(s) Multiply M x Voi Store Vti Increment pointers (i) to next Voi, next Vti Decrement vector counter If vectors remain, Jump to MxV End
The critical section is the MxV loop. For a typical object with hundreds of polygons, it is repeated thousands of times. It must be as efficient (fast) as possible. This subject is discussed at length in Section 3.2 .
When using MMX technology for graphics applications, the limitations of integer arithmetic must be carefully considered and managed. The programmer may need to explicitly scale data at each step, to make full use of the available precision, while avoiding overflows. 16-bit integer precision is sufficient for most components of computer graphics; angles can be resolved to about 1/1000º, and screen coordinates to about 1/50 pixel.
16-bit precision is not sufficient for large global graphics databases where good accuracy must be maintained both for individual objects, and between objects a great distance apart. For large global graphics databases, 32-bit precision is needed for the world space, while 16-bit precision is still adequate for local object coordinates. This scheme could be implemented in MMX technology by adding a 32-bit world space translation to the 32-bit results (see the last line of Figure 2). The 16-bit translation shown in this paper is essentially free, since the PMADDWD instruction operates on four elements at a time.
Typical 3D software (i.e., CAD and drawing) packages produce vertex and transform data in floating-point format, which is converted to integer for MOVD processing. Vertex data is converted once, with the integer values stored for repeated use. Transform data is better left in floating-point, so that it can be repeatedly modified without accumulating error. Each time the transform matrix is recalculated, the transform data is converted to integer. Floating point is also advantageous here because standard sine and cosine routines are in floating point, and recalculating the matrix on the Pentium® processor is faster in floating point than in scalar integer.
The sample C languageprogram shown in Section 4.1 uses a floating point space, with limits chosen so that matrix coefficients do not exceed approximately ±4.0. Vertex and matrix data sent to the signed 16-bit integer routine are re-scaled from ±4.0 to ±32K. As such, transformed vector data returned from the routine requires a re-scaling of *4, for best use of precision. This shift can be done in the routine for no extra cost, by adjusting the amount of shift in the 32-bit to 16-bit conversion (see Listing 1A, lines 20, 27, 34).
The speed of MOVD routines, like other assembly code routines, can benefit greatly from hand optimization. This MOVD routine benefited most from these optimizations:
Pairing: Re-ordering instructions to make better use of both of the Pentium processor super-scalar pipelines. MMX instructions are similar to scalar integer instructions, in that they can be executed two at a time, if certain microarchitecture constraints are met. These constraints are codified into "pairing rules."
Data alignment: Ensuring that memory reads and writes do not cross their natural alignment boundaries. For instance, the 64-bit MOVD memory accesses should be done to 8-byte-aligned memory addresses. If a boundary is crossed, the routine stalls, while the processor makes an extra memory access.
Loop unrolling: A loop is unrolled by writing it out "N" times, with each new, longer loop executed only 1/Nth as many times. Loop unrolling helps pair instructions at the (original) loop edges, and reduces the average cost-per-loop of jump instructions. This routine was eventually determined not to be a good candidate for loop unrolling, since most of its instructions were eventually paired, and the jump instruction is only 1/15th of the loop count (after the first mis-predicted jump). Since each of the three row calculations are independent, they can be interleaved within the loop (see Example 3), accomplishing much of the benefit of loop unrolling.
The general procedure is to first create a straightforward MOVD routine, which is easy to understand and debug, then optimize that routine in successive steps. Correct operation is verified throughout the optimization process by comparing the results (e.g. hundreds of test vectors) of the MOVD routine to a similar routine coded in the C language(see Appendix B).
As a further check, input data (matrix and vectors) are compared before and after the routine, to make sure they are not accidentally modified.
All input data is assumed to be in L1 cache, properly aligned. Such data is accessible with no memory stalls.
The Pentium processor's 16 Kbyte L1 data cache can hold input and output vertices for about 1000 polygons. While this is adequate for simple animation scenes, more complex applications requires access to L2 cache or main memory.
Data alignment is easily achieved by declaring the critical arrays first, in Microsoft Visual C. A more robust method would be to explicitly check data alignment at run-time, and re-align it then, if necessary.
The hand optimization effort is concentrated on the critical loop discussed above. Any cycle time saved in this loop is greatly magnified, as the loop executes on the order of thousands of times. Code outside of this loop (subroutine call/return, parameter retrieval, constant matrix setup) is executed only once per call, so did not merit much optimization effort.
Each stage of optimization consisted of:
Re-ordering instructions for pairing and stall avoidance.
Verifying continued correct operation, by comparing to the C routine.
Using simulation tools to verify that the desired pairings and timings were accomplished.
These optimization stages are laid out in the next few pages. Each "listing" here actually represents two or three small optimization passes.
Listing 1A shows the original MOVD routine (MASM assembly language source code with line numbers added), coded for straight-forward understanding and debugging. (Note: in Listing 1A, lines are spaced to generally show small logical blocks. In other listings, lines are spaced to show super-scalar pairing).
1 INCLUDE iammx.inc ;macros for new MMX instructions 2 .486P ;enable all 486 instructions, FLAT 3 .model FLAT ;single 32-bit flat memory 4 .CODE ;begin code portion of segment 5 _MxV_mmx PROC PUBLIC ;MSVC linker mangles name to _MxV_mmx ;C requires ebp,esi,edi preserved. This routine doesn't use them. ;get pointers to parameters 6 mov eax,[esp]+ 4 ;eax = ptr to matrix 7 mov ebx,[esp]+ 8 ;ebx = ptr to vector 8 mov ecx,[esp]+12 ;ecx = numvec 9 mov edx,[esp]+16 ;edx = ptr to result ;Load entire 3x4 matrix 10 movq mm0, 0[eax] ;Matrix row 0 (4 16-bit elements) 11 movq mm1, 8[eax] ;Matrix row 1 (4 16-bit elements) 12 movq mm2,16[eax] ;Matrix row 2 (4 16-bit elements) 13 NextVect: 14 movq mm3,[ebx] ;Load vector (4 16-bit elements) ;Row0 x vector = Result0 15 movq mm4,mm3 ;make working copy of vector 16 pmaddwd mm4,mm0 ;multiply row0 x vector 17 movq mm5,mm4 ;add high and low order 32-bit results 18 psrlq mm5,32 19 paddd mm4,mm5 20 psrad mm4,15-2 ;Shift 32 to 16; also app-specific <<2 21 movd [edx],mm4 ;Store first (16-bit) element of result ;Row1 x vector = Result1 22 movq mm4,mm3 ;make working copy of vector 23 pmaddwd mm4,mm1 ;multiply row0 x vector 24 movq mm5,mm4 ;add high and low order 32-bit results 25 psrlq mm5,32 26 paddd mm4,mm5 27 psrad mm4,15-2 ;Shift 32 to 16; also app-spec <<2 28 movd [edx]+2,mm4 ;Store secnd (16-bit) element of result ;Row2 x vector = Result2 29 movq mm4,mm3 ;make working copy of vector 30 pmaddwd mm4,mm2 ;multiply row0 x vector 31 movq mm5,mm4 ;add high and low order 32-bit results 32 psrlq mm5,32 33 paddd mm4,mm5 34 psrad mm4,15-2 ;Shift 32 to 16; also app-spec <<2 35 movd [edx]+4,mm4 ;Store third (16-bit) element of result ;Loop to next vector, or quit 36 add ebx,8 ;advance to next input vector 37 add edx,6 ;advance to next output vector 38 dec ecx ;if not counted through all vectors 39 jnz NextVect ; then loop back to do the next one. 40 emms ;exit multimedia (clear fp reg valids) 41 ret 0 42 _MxV_mmx ENDP 43 END
Listings 1B through 5 are in a format similar to that produced by the WDIS static disassembler and simulator tool. WDIS is useful for analyzing pairing, cycle counts and most stall penalties. Example 4 shows this format: the two instructions (InstrA and InstrB) are displayed with no intervening blank line to indicate that they were paired. InstrB has a cycle count of "1-1" (one minus one, or zero), meaning it executes in the same cycle as InstrA. The other columns show the explanations for non-pairing and for stall penalties. (For a full explanation of WDIS, refer to the WDIS documentation).
# Instruction Clocks Reason non-pair Stall Penalties > 1 instrA 1 2 instrB 1 - 1
Listing 1B shows the simulation results for the critical loop from Listing 1A.
# Instruction Clocks Reason no-pair Stall Penalties NextVect: 1 movq mm3, [ebx] 1 BBstart, MM-Int 2 movq mm4, mm3 1 DepExpSrc_mm3 3 pmaddwd mm4, mm0 1 DepExpDst_mm4 4 movq mm5, mm4 3 DepExpSrc_mm4 PMUL_Dep:2 5 psrlq mm5, 32 1 DepExpDst_mm5 6 paddd mm4, mm5 1 DepExpSrc_mm5 7 psrad mm4, 13 1 DepExpDst_mm4 8 movd [edx], mm4 2 DepExpSrc_mm4,MM-Int MM_MOV_Dep:1 9 movq mm4, mm3 1 - 1 10 pmaddwd mm4, mm1 1 11 movq mm5, mm4 3 DepExpSrc_mm4 MM_PMUL_Dep:2 12 psrlq mm5, 32 1 DepExpDst_mm5 13 paddd mm4, mm5 1 DepExpSrc_mm5 14 psrad mm4, 13 1 DepExpDst_mm4 15 movd [edx+2], mm4 2 DepExpSrc_mm4, MM-Int MM_MOV_Dep:1 16 movq mm4, mm3 1 - 1 17 pmaddwd mm4, mm2 1 18 movq mm5, mm4 3 DepExpSrc_mm4 MM_PMUL_Dep:2 19 psrlq mm5, 32 1 DepExpDst_mm5 20 paddd mm4, mm5 1 DepExpSrc_mm5 21 psrad mm4, 13 1 DepExpDst_mm4 22 movd [edx+4], mm4 2 DepExpSrc_mm4,MM-Int MM_MOV_Dep:1 23 add ebx, 8 1 PrevMM-Int 24 add edx, 6 1 - 1 25 dec ecx 1 26 jnz NextVect 1 - 1 Total Cycles: 31
The critical loop time was 31 cycles. Of the 26 instructions, only four (9, 16, 24, and 26) were paired, producing a Cycles Per Instruction (CPI) measure of about 1.2. Given the Pentium processor's two pipelines, the ideal CPI would be 0.5. This provides the hint that better pairing should be possible.
The routine was re-written to allow pairing at lines 4, 5, 6, 11, 12, 13 and 18, 19, 20. Reversing register usage eliminated dependencies. Several other simple re-ordering attempts failed to produce better pairing than that shown in Listing 2.
# Instruction Clocks Reason no-pair Stall Penalties NextVect: 1 movq mm4, [ebx] 1 2 movq mm3, mm4 1 DepExpSrc_mm4 3 pmaddwd mm4, mm0 1 - 1 4 movq mm5, mm4 3 MM_PMUL_Dep:2 5 psrlq mm4, 32 1 - 1 6 paddd mm5, mm4 1 7 psrad mm5, 13 1 DepExpDst_mm5 8 movd [edx], mm5 2 DepExpSrc_mm5,MM-Int MM_MOV_Dep:1 9 movq mm4, mm3 1 - 1 10 pmaddwd mm4, mm1 1 11 movq mm5, mm4 3 DepExpSrc_mm4 MM_PMUL_Dep:2 12 psrlq mm4, 32 1 - 1 13 paddd mm5, mm4 1 14 psrad mm5, 13 1 DepExpDst_mm5 15 movd [edx+2], mm5 2 DepExpSrc_mm5,MM-Int MM_MOV_Dep:1 16 movq mm4, mm3 1 - 1 17 pmaddwd mm4, mm2 1 18 movq mm5, mm4 3 DepExpSrc_mm4 MM_PMUL_Dep:2 19 psrlq mm4, 32 1 - 1 20 paddd mm5, mm4 1 21 psrad mm5, 13 1 DepExpDst_mm5 22 movd [edx+4], mm5 2 DepExpSrc_mm5,MM-Int MM_MOV_Dep:1 23 add ebx, 8 1 PrevMM-Int 24 add edx, 6 1 - 1 25 dec ecx 1 26 jnz NextVect 1 - 1 Total Cycles: 27
At this point, pairing has decreased the CPI to about 1.0, for a total of 27 cycles. Not much more can be done with this routine, while maintaining the existing sequence of finishing one row before starting the next. Besides non-paired instructions, two trouble spots are particularly costly:
As the two-cycle (PMADDWD) stall is worse, it is advantageous to deal with it first, then deal with any remaining stalls later.
Avoiding each two-cycle stall, or dead time, amounts to finding some useful work (instructions) to take place during the two cycles after each PMADDWD issues. But, within the calculations of any one of the three rows, each instruction is dependent on the previous one, so none of these can be re-ordered. The solution is a more complete re-structuring of the entire routine.
Due to the dependencies in this algorithm, the only instruction that can be executed without delay after a PMADDWD instruction, is the PMADDWD instruction of a different row. Note that, while a given PMADDWD instruction takes three cycles to complete, succeeding PMADDWD instructions may be issued every cycle. After the third PMADDWD instruction is issued, the results from the first will be available (more MM registers must be used to simultaneously hold the three separate rows' data). This general notion of staggering (or pipelining) the three rows' calculations can hold through the subsequent calculations, avoiding other dependencies, as shown in Figure 3.
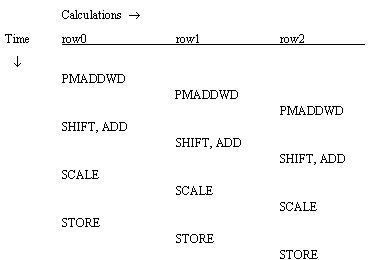
Listing 3 shows this new algorithm structure.
# Instruction Clocks Reason no-pair Stall Penalties NextVect: 1 movq mm3, [ebx] 1 2 movq mm4, mm3 1 DepExpSrc_mm3 3 movq mm5, mm4 1 DepExpSrc_mm4 4 pmaddwd mm3, mm0 1- 1 5 pmaddwd mm4, mm1 1 6 pmaddwd mm5, mm2 1 MM_Multiplier 7 movq mm6, mm3 2 - 1 MM_PMUL_Dep:1 8 psrlq mm3, 32 1 9 paddd mm3, mm6 1 DepExpDst_mm3 10 movq mm6, mm4 1 - 1 11 psrlq mm4, 32 1 12 paddd mm4, mm6 1 DepExpDst_mm4 13 movq mm6, mm5 1 - 1 14 psrlq mm5, 32 1 15 paddd mm5, mm6 1 pExpDst_mm5 16 psrad mm3, 13 1 - 1 17 psrad mm4, 13 1 18 psrad m5, 13 1 Shift 19 movd edx], mm3 1 M-Int 20 movd [edx+2], mm4 1 MM-Int 21 movd [edx+4], mm5 1 MM-Int 22 add edx, 6 1 PrevMM-Int 23 add ebx, 8 1 - 1 24 dec ecx 1 25 jnz NextVect 1 - 1 Total Cycles: 19
This restructuring immediately reduces cycle count by about one third: Instructions are reduced to 25, since moves between MM registers are done more efficiently. Seven instructions are paired. CPI is about 0.8, for a total cycle count of 19.
The overall staggered (pipelined) structure eliminates not only the PMADDWD stalls, but also the MM - memory stalls (Listing 2, lines 8, 15, and 22). The stall at line 7 appears only because the instruction was (unexpectedly) paired with the third PMADDWD. This will be resolved in the final version. (Note: during the next one or two optimization passes, it may be useful to insert a NOP instruction after line 6, to force the later instructions to pair differently. By the final optimization pass, the NOP ought to be replaced by some useful instruction.)
The next step is to pair as many remaining instructions as possible (the big restructuring of step 3 produced new opportunities):
Instruction 20 is hidden by moving it above instruction 18. More pairing of this sort is not allowed, since the MM register data from the shifts must be available one cycle in advance.
Instruction 22 is hidden by moving it up to pair with instruction 6. (The previous pairing of instruction 7 with instruction 6 did not save any cycles because of a data dependency stall.) The ADD EDX,6 can precede the movd [EDX],mm instructions, if all MOVD addresses are adjusted by -6.
Instruction 23 is hidden by moving it up to pair with instruction 11.
The result is shown in Listing 4.
# Instruction Clocks Reason no-pair Stall Penalties NextVect: 1 movq mm3, [ebx] 1 2 movq mm4, mm3 1 DepExpSrc_mm3 3 pmaddwd mm3, mm0 1 - 1 4 movq mm5, mm4 1 5 pmaddwd mm4, mm1 1 - 1 6 pmaddwd mm5, mm2 1 7 add ebx, 6 1 - 1 8 movq mm6, mm3 1 9 psrlq mm3, 32 1 - 1 10 paddd mm3, mm6 1 11 movq mm6, mm4 1 - 1 12 psrlq mm4, 32 1 13 add edx, 8 1 - 1 14 paddd mm4, mm6 1 15 movq mm6, mm5 1 - 1 16 psrlq mm5, 32 1 17 paddd mm5, mm6 1 DepExpDst_mm5 18 psrad mm3, 13 1 - 1 19 psrad mm4, 13 1 20 movd [edx-6], mm3 1 MM-Int 21 psrad mm5, 13 1 - 1 22 movd [edx-4], mm4 1 23 movd [edx-2], mm5 1 MM-Int 24 dec ecx 1 PrevMM-Int 25 jnz NextVect 1 - 1 Total Cycles: 15
The resulting loop time is 15 cycles. This is less than half of the original cycle count of 31 (see Listing 1B). CPI is 0.6, which is close to ideal.
At this point, all stalls appear to have been eliminated but, in reality, one problem area remains: misaligned memory writes. Writes from MMX registers (lines 20, 22, and 23) are 32 bits (even though this routine only uses 16-bits from each). When writing to 4-byte misaligned addresses, which happens every other write, a three cycle stall occurs. These stalls do not show up in the WDIS static disassembler, because it does not know the runtime values of [EDX]. The CCMMX dynamic simulator (operating on traces generated by the KTR tracer) shows these stalls. They cost 4.5 cycles per row (beyond the 15 shown by WDIS), increasing loop time by 30%.
The stalls can be eliminated by writing only to 4-byte boundaries. One way to do this is to use 32 bits to store the first two 16-bit results, and 32 its to store the third 16-bit result. Half of the second 32 its is unused, so output memory consumption is 33% more. This method is shown in Listing 5.
# Instruction Clocks Reason no-pair Stall Penalties NextVect: 1 movq mm3, [ebx] 1 BBstart, MM-Int 2 movq mm4, mm3 1 DepExpSrc_mm3 3 pmaddwd mm3, mm0 1 - 1 4 movq mm5, mm4 1 5 pmaddwd mm4, mm1 1 - 1 6 pmaddwd mm5, mm2 1 7 add ebx, 8 1 - 1 8 movq mm6, mm3 1 9 psrlq mm3, 32 1 - 1 10 paddd mm3, mm6 1 11 movq mm6, mm4 1 - 1 12 psrlq mm4, 32 1 13 dd edx, 8 1 - 1 14 psrad mm3, 13 1 15 paddd mm4, mm6 1 - 1 16 psrad mm4, 13 1 17 movq mm6, mm5 1 - 18 psrlq mm5, 32 1 19 punpcklwd mm3, mm4 1 MM_Shift 20 paddd mm5, mm6 1 - 1 21 psrad mm5, 13 1 22 movd [edx-8], mm3 1 MM-Int 23 movd [edx-4], mm5 1 MM-Int 24 dec ecx 1 PrevMM-Int 25 jnz Block1_1 1 - 1 Total Cycles: 15
The PUNPCKLWD instruction (line 19) is used to move word0 of MM4 into word1 of MM3. Both 16-bit results are then stored together (line 22). Careful pairing allows this extra functionality without increasing the cycle count. (Note that PUNPCKLWD uses the MMX technology "shift" functional block, which is used in every cycle from line 8 to line 21.)
This is probably close to the optimum code for this particular problem. (An even more memory-efficient solution could be done by packing two 16-bit results into every 32-bit memory location. This would requires unrolling the loop, since one loop produces only three results.) The complete MASM assembly source code listing is in Appendix A.
As a general point of comparison, it is interesting to observe the cycle counts of equivalent compiler-optimized C code. An integer and a floating-point matrix multiply routine were each coded in C, as shown in Example 5.
for (i=0; i<200; i++)
{
R[i][0] = M[0][0]*V[i][0] + M[0][1]*V[i][1] + M[0][2]*V[i][2] + [0][3]*V[i][3];
R[i][1] = M[1][0]*V[i][0] + M[1][1]*V[i][1] + M[1][2]*V[i][2] + [1][3]*V[i][3];
R[i][2] = M[2][0]*V[i][0] + M[2][1]*V[i][1] + M[2][2]*V[i][2] + [2][3]*V[i][3];
}
The Microsoft Visual C++ (MSVC) compiler to generate its fastest code, then cycle counts were traced for the cases of data already in cache (hot) and data not in cache (cold). "Pentium" processor is a particular setting on the MSVC compiler that may or may not be set. In this case it was specifically set, and that is significant for the results that follow. As shown in Figure 4, the MOVD routine ran about three times faster than the floating-point C code, and 5 to 10 times faster than the integer C code.
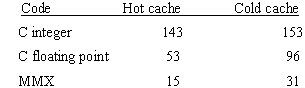
A simple program (3DDEMO.EXE) is included to demonstrate the use of MMX technology to perform 3D geometry transform calculations. The program is written in Microsoft Visual C and runs under a 32-bit windows operating system, such as Microsoft Windows 95. Its 3D data consists of 16 vertices, formed into four polygons, chosen to form a cube. As the user changes geometry parameters (rotation, translation, etc.) with mouse and keyboard, the cube data is transformed and redrawn in real time. A window menu option allows the user to select either scalar integer (C) or SIMD integer (MOVD) to perform the 3D geometry transforms. The program was purposely sized and scaled to represent the limitations of integer arithmetic. The integer range is mapped to the window edges. Moving any vertex beyond a window edge causes it to "wrap around."
More instructions are included in a window menu option in the program.
This study has demonstrated how MMX technology can be successfully used to accelerate 3D geometry transforms. The MMX instruction set was shown to map well to 3D graphics calculations. The process of hand optimization was detailed. Hand-optimized code was on the order of twice as fast as naive (un-optimized) code. The optimized MOVD code ran at least three times faster than equivalent compiler-optimized C (scalar) code. This order of speedup is significant for compute-bound operations.
While the exact requirements of particular graphics applications will vary, MMX technology is generally applicable. When applied to stages of a graphics pipeline such as geometry, lighting, and rendering, Intel's MMX technology provides an opportunity for a new level of software graphics performance on PCs.
The following is a ource listing (MASM 6.11d format) of the completed MOVD routine.
Matrix-vector multiplication for 3D geometry transforms are shown.
The lines in the critical loop are spaced to show actual pairing.
INCLUDE iammx.inc ;to parse MMX instructions .486P ;enable all 486 instructions (enable FLAT) .model FLAT ;single 32-bit flat memory segment .CODE _MxV_mmx PROC PUBLIC ;MSVC linker mangles MxV_mmx to _MxV_mmx ;C requires ebp,esi,edi preserved. This routine doesn't use them. ;get pointers to parameters mov eax,[esp]+ 4 ;eax = ptr to matrix mov ebx,[esp]+ 8 ;ebx = ptr to vector mov ecx,[esp]+12 ;ecx = numvec mov edx,[esp]+16 ;edx = ptr to result ;Load entire 3x4 matrix movq mm0, 0[eax] ;Matrix row 0 (4 16-bit elements) movq mm1, 8[eax] ;Matrix row 1 (4 16-bit elements) movq mm2,16[eax] ;Matrix row 2 (4 16-bit elements) NextVect: movq mm3,[ebx] ;Load vector (4 16-bit elements) into reg movq mm4,mm3 ;copy to other regs for use by 3 pmadds pmaddwd mm3,mm0 ;multiply row0 X vector movq mm5,mm4 pmaddwd mm4,mm1 ;multiply row1 X vector pmaddwd mm5,mm2 ;multiply row2 X vector add ebx,8 ;increment to next input vector movq mm6,mm3 ;add row0 high and low order 32-bit results psrlq mm3,32 ; paddd mm3,mm6 ; movq mm6,mm4 ;add row1 high and low order 32-bit results psrlq mm4,32 ; add edx,8 ;increment (in advance) to next result psrad mm3,15-2 ;Shift 32 to 16; also app. specific <<2 paddd mm4,mm6 ; psrad mm4,15-2 ;Shift 32 to 16; also app. specific <<2 movq mm6,mm5 ;add row2 high and low order 32-bit results psrlq mm5,32 ; punpcklwdmm3,mm4 ;Copy word0 of mm4 into word0 of mm3 paddd mm5,mm6 ; psrad mm5,15-2 ;Shift 32 to 16; also app. specific <<2 movd [edx]-8+0,mm3 ;Store 1st and 2nd elements, one 32-bit write movd [edx]-8+4,mm5 ;Store 3rd (and unused 4th) 16-bit element dec ecx ;if not counted through all the vectors jnz NextVect ;then loop back to do the next one. emms ;end MMX stae (remove fp reg valids) ret 0 _MxV_mmx ENDP END
The following is a source listing (MSVC 2.0 format) of the C program used to test the MMX optimized code.
/*
3DMMX test driver JAS 1/96
*/
#include <stdio.h>
#include <stdlib.h> //for rand,srand
#include <time.h> //for time
#define NumVec 200
/* Function prototypes */
void MxV_mmx(short matrix[3][4], short vector[NumVec][4],
short NV, short result[NumVec][4]);
void MxV_sca(short matrix[3][4], short vector[NumVec][4],
short NV, short result[NumVec][4]);
/* Declared globally for easy 8byte alignment */
short matrix [3][4];
short vector [NumVec][4];
short result_mmx[NumVec][4];
short result_sca[NumVec][4];
/*
** Main
** Inputs : none
** Outputs : (display) results of Matrix X Vector multiply
** Called by : (startup)
*/
void main( )
{
int h,i,j;
char dummy;
short vec_bak[NumVec][4];
short mat_bak [3][4];
int mat_err,vec_err;
/* Notify, if any vars are mis-aligned */
if ( ((long)matrix %8) || ((long)vector %8) ||
((long)result_mmx%8) || ((long)result_sca%8) )
{
printf("'matrix ' is at %ld\n",(long)vector %8);
printf("'vector ' is at %ld\n",(long)vector %8);
printf("'result_mmx' is at %ld\n",(long)result_mmx%8);
printf("'result_sca' is at %ld\n",(long)result_sca%8);
printf("\n[ENTER] to continue\n"); dummy=getchar( );
}
/* Initialize input variables to random values */
srand((unsigned)time(NULL)); //reseed random number generator
for (i=0; i<3 ; i++) for (j=0; j<4; j++)
matrix[i][j] = (-16384 + rand())>>2;
for (h=0; h<NumVec; h++) for (j=0; j<4; j++)
vector[h][j] = (-16384 + rand())>>2;
/* Save backup for error check */
for (i=0; i<3 ; i++) for (j=0; j<4; j++) mat_bak[i][j]=matrix[i][j];
for (h=0; h<NumVec; h++) for (j=0; j<4; j++) vec_bak[h][j]=vector[h][j];
mat_err = vec_err = 0;
/* Call the MMX technology version */
MxV_mmx(matrix, vector, NumVec, result_mmx);
/* Error check: make sure input data didn't get clobbered */
for (i=0; i<3 ; i++) for (j=0; j<4; j++)
mat_err+= (matrix[i][j]!=mat_bak[i][j]);
for (h=0; h<NumVec; h++) for (j=0; j<4; j++)
vec_err+= (vector[h][j]!=vec_bak[h][j]);
if (mat_err)
{
printf("Error: MMX altered Matrix\nPress [ENTER]\n"); dummy=getchar();
}
if (vec_err)
{
printf("Error: MMX altered Vector\nPress [ENTER]\n"); dummy=getchar();
}
/* Call the scalar version */
MxV_sca (matrix, vector, NumVec, result_sca) ;
/* Display and compare the results from each version */
for (h=0; h<NumVec; h++)
{
printf("#%2d: Sca= %6d %6d %6d \t %6d %6d %6d =MMx ",
h, result_sca[h][0], result_sca[h][1], result_sca[h][2],
result_mmx[h][0], result_mmx[h][1], result_mmx[h][2]);
if ( (result_sca[h][0]!=result_mmx[h][0]) ||
(result_sca[h][1]!=result_mmx[h][1]) ||
(result_sca[h][2]!=result_mmx[h][2]) )
printf(" Error! \7");
printf("\n");
}
printf ("\n[ENTER] to continue\n"); dummy=getchar();
}
/*
** C (scalar integer) version of matrix x vector multiply
** Simulate the MMX technology results
*/
void MxV_sca (short M[3][4], short V[NumVec][4], short nv, short result[NumVec][4])
{
short h,i,j;
long sum;
for (h=0; h<nv; h++)
{
for (i=0; i<3; i++)
{
sum = 0;
for (j=0; j<4; j++)
{
sum += (long)M[i][j] * V[h][j];
}
result[h][i] = (short)(sum>>13);
}
}
}